Задача 5-4-1-32

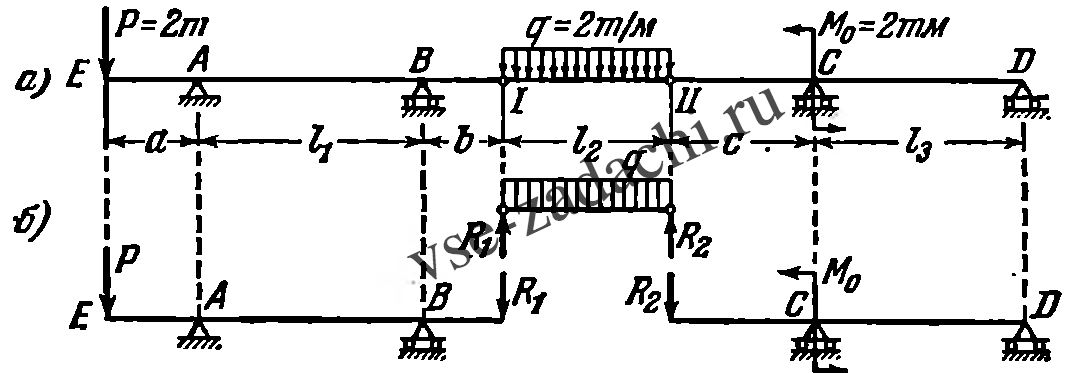
Построить эпюры поперечных сил и изгибающих моментов для четырехопорной балки с двумя промежуточными шарнирами, изображенной на схеме. Вычислить наибольшие ординаты эпюр Q и M, если a = 2 м, b = 1 м, c = 3 м, l₁ = 4 м, l₂ = 3 м и l₃ = 4 м.

Указание. Проще всего расчленить балку на подвесную (I—II) и две основные (E—I и II—D), как показано на схеме б. Заменив давления, передающиеся от подвесной балки через шарниры, реакциями R₁ и R₂, вычисленными для двухопорной балки I—II, построить эпюры Q и М для каждой из балок в отдельности.

Можно поступить и иначе. Так как изгибающий момент в шарнире равен нулю (шарнир момента передать не может), то в дополнение к уравнениям статики для всей системы можно составить уравнения моментов относительно шарниров I и II (рассматривая силы, расположенные слева или справа от них) и приравнять их нулю. Эго позволит определить все опорные реакции и строить эпюры Q и M обычным путем, как для бесшарнирной балки.