Задача 5-2-3-39

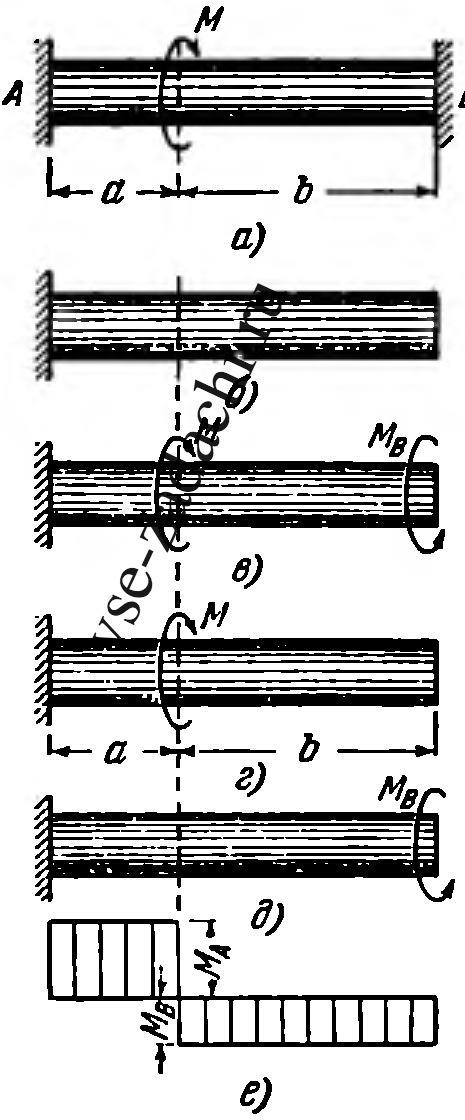
Концы стержня круглого сечения защемлены; в промежуточном сечении приложена пара сил с моментом M = 1200 кгм (см. рисунок, схема а). Расстояние b = 2a. Чему равны наибольшие касательные напряжения в стержне, если его диаметр 8 см?

Указание. Уравнение статики: M_A + M_B = M. Система однажды статически неопределима. Выберем за основную (статически определимую) систему стержня схему б. При загружении этой схемы парами M и М_B (схема в) и при условии, что φ_B = 0, схема в станет эквивалентной схеме а. Рассмотрим теперь раздельно действие на стержень пары M (схема г) и пары M_B (схема д). Сечение B в схеме г повернется yа угол φ’_B = Ma/(GJ_p) в схеме д поворот того же сечения φ’’_B = M_B(a + b)/(GJ_p) (в другую сторону). Но так как φ_B = φ’_B + φ’’_B = 0, находим MB = aM/(a + b), а M_A = bM/(a + b). Строим эпюру крутящего момента (e). Из эпюры видно, что на левом участке касательные напряжения больше, чем на правом.