Задача 5-4-4-24

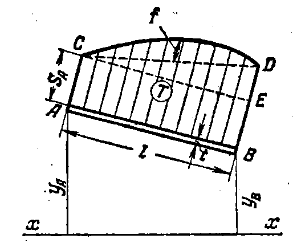
Для произвольной прямой полоски AB, выделенной из сечения тонкостенного стержня, известны ординаты ее концов y_A и y_B, площадь полоски F = lt и ординаты S_A эпюры S_x, равная статическому моменту относительно оси x части сечения, расположенной до точки A. Показать, что площадь T эпюры S_x, приходящейся на полоску AB, можно вычислять по формуле

T = [S_A + F(2y_A + y_B)/6]l

независимо от того, очерчена ли эпюра S_x по выпуклой или по вогнутой параболе.